Solving VIP for oriented graphs

Let G=(V,E) be a graph. For a subset A of V denote by ball(A) the set of all graph vertices at distance at most 1 from A. The Vertex Isoperimetric Problem (VIP) consists of finding for a given m a subset A of V such that |A| = m and |ball(A)| is minimum among all subsets of size m. This minimum size of the ball is denoted by ball(m). For more information on the VIP please check the survey [1].

The VIP is NP-complete, so there is no much hope for its efficient solution. This program simply generates all subsets of V, by using the Gray code approach for generating all subsets of a set, and computes the size of the ball about each of these subsets. Therefore, the number of vertices in the graph should not exceed 25 to get a solution within several minutes, depending on the graph. Solution for a larger graph is possible is the graph can be factorized by using the cartesian product operation (see here for details).

The program also checks whether or not the graph admits nested solutions. If nested solutions exist, one of optimal total orders is presented. Otherwise, a longest initial series of nested solutions is output.

To use this tool you should prepare a file with your graph encoding (see below for instructions) and upload this file for processing. The adjacency list for each vertex should consist of the vertices reachable by outgoing edges from that vertex.

References

[1] S.L. Bezrukov: Isoperimetric problems in discrete spaces, in: Extremal Problems for Finite Sets., Bolyai Soc. Math. Stud. 3, P. Frankl, Z. Füredi, G. Katona, D. Miklos eds., Budapest 1994, 59-91.

Select a file to upload

Graph encoding instructions

The graphs are encoded by using the adjacency list represenation. The graph file is a text (ASCII) file with the number of lines equal to the number of vertices, that is one line per vertex. For each vertex v of G the corresponding line must contain the following information:

label label₁ label₂ . . . label_k

Here:

label is the label of v (a string consisting of letters, digits or the underscore symbols "_" only)
label₁ label₂ . . . label_k is a list of labels of vertices advacent with v. Isolated vertices are not allowed.

Moreover, the file must satisfy the following claims:

- The file size must not exceed 50 kilobytes.
- The parameters within one line must be separated by one or more spaces.
- Empty lines are ignored.
- A portion of a line followed by the # sign is considered as a comment and ignored. The comments are optional.

Example

Graph	Encoding	Comments
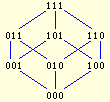	000 001 010 100 # the bottom vertex 001 000 011 101 # first level 010 000 011 110 100 000 101 110 011 001 010 111 # second level 101 001 100 111 110 010 100 111 111 011 101 110 # the top vertex	empty line, ignored vertex with label 001 is adjacent to vertices with labels 000, 011, and 101 the top vertex is advacent to 3 vertices

Graph

Encoding

Comments

000 001 010 100  # the bottom vertex

001 000 011 101  # first level
010 000 011 110
100 000 101 110
011 001 010 111  # second level
101 001 100 111
110 010 100 111
111 011 101 110  # the top vertex

 
empty line, ignored
vertex with label 001 is adjacent
   to vertices with labels 000,
   011, and 101



the top vertex is advacent to 3 vertices

Isoperimetric Tools