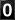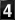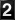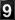Isoperimetric Tools

Solution of the VIP for the Cartesian product of two graphs

This tool is intended for solving the Vertex Isoperimetric Problem (VIP) on the cartesian product of two graphs. See here for the problem statement. The cartesian product G x H of graphs G and H is defined as follows. The vertex set of G x H is the cartesian product of the vertex sets of G and H, and the pairs (p₁, q₁) and (p₂, q₂) form an edge in G x H iff p₁ = p₂ and (q₁, q₂) is an edge of H, or q₁ = q₂ and (p₁, p₂) is an edge of G.

It is assumed that the graphs G and H admit nested solutions in VIP, and a solution of the VIP problem is known for each of them. That is, it is assumed that one knows the values ball_G(k) and ball_H(m) for each k = 1 . . |G| and m = 1 . . |H|.

To apply this tool, enter the values of the VIP function for G and H. That is, one has to enter the minimum size of a ball for each cardinality for G and H. The default values of the ball sizes in the input fields below correspond to the wheel graph W₄.

Clicking on the button causes sending your input to the server for processing. The processing consists of generating all ideals of the |G| x |H| grid and computing the size of the ball about each of them. Since the number of ideals equals the order of the poset L(|G|, |H|), which is the binomial coefficient C(|G|+|H|, |G|), the computations might take some time.

After computing the VIP values for G x H for each value of the cardinality, the program checks for the existence of nested solutions and shows one of the longest nested series. If nested solutions exist for each value of the cardinality, the program will search for an order that additionally satisfies the continuity property.