Isoperimetric Tools
Solution of the EIP problem
Let G=(V,E) be a graph. For a subset A of V denote
by cut(A) the edge-cut separating A from its complement in
V, and by E(A) the set of graph edges induced by the vertex
set A. There are two versions of the Edge Isoperimetric Problem (EIP):
- For for a given number m, find a subset A of V
such that |A| = m and |cut(A)| is minimum among all subsets
of size m. This minimum size of the edge-cut is denoted by
cut(m).
- For for a given number m, find a subset A of V
such that |A| = m and |E(A)| is maximum among all subsets
of size m. This maximum value of |E(A)| is denoted by
E(m).
These problems are equivalent for k-regular graphs due to the
identity
2·|E(A)| + |cut(A)| = k·|A|
That is, for regular graphs any solution to one of these problem is also a
solution to the other one.
For non-regular graphs the above identity is not valid and the problems might
have different solutions. For more information on the EIP please refer to
the survey [1].
The EIP is NP-complete, so there is no much hope for its efficient solution.
This program simply generates all subsets of V, by using
the Gray code approach for generating all subsets of a set, and
computes the size of the edge-cut (resp. the number of induced edges) for
each of these subsets.
Therefore, the number of vertices in the graph should not exceed 25 to get a
solution within several minutes, depending on the graph. Solution for a
larger graph is possible is the graph can be factorized by using the cartesian
product operation (see here for details).
The program also checks whether or not the graph admits nested solutions.
If nested solutions exist, one of the optimal total orders is presented.
Otherwise, a longest initial series of nested solutions is output.
To use this tool you should prepare a file with your graph encoding (see
below for instructions) and upload this file for processing. Also make sure
to choose the desired version of the EIP.
The program also checks whether or not the graph admits nested solutions.
If nested solutions exist, one of optimal total orders is presented.
Otherwise, a longest initial series of nested solutions is output.
To use this tool you should prepare a file with your graph encoding
and upload this file for processing (see the encoding instructions below).
References
[1] S.L. Bezrukov: Edge isoperimetric problems
on graphs, in: Graph Theory and Combinatorial Biology, Bolyai Soc.
Math. Stud. 7, L. Lovasz, A. Gyarfas, G.O.H. Katona, A. Recski, L. Szekely
eds., Budapest 1999, 157-197.
Select a file to upload
Graph encoding instructions
The graphs are encoded by using the adjacency list represenation.
The graph file is a text (ASCII) file with the number of lines equal to the
number of vertices, that is one line per vertex. For each vertex
v of G the corresponding line must contain the following
information:
label
label1 label2 . . .
labelk
Here:
label is the label of v
(a string consisting of letters, digits or the underscore symbols "_"
only)
label1 label2 . . .
labelk is a list of labels of vertices advacent
with v. Isolated vertices are not allowed.
Moreover, the file must satisfy the following claims:
- The file size must not exceed 50 kilobytes.
- The parameters within one line must be separated by one or more spaces.
- Empty lines are ignored.
- A portion of a line followed by the # sign is considered as a comment
and ignored. The comments are optional.
Example
| Graph | Encoding | Comments |
|---|
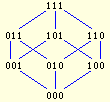 |
000 001 010 100 # the bottom vertex
001 000 011 101 # first level
010 000 011 110
100 000 101 110
011 001 010 111 # second level
101 001 100 111
110 010 100 111
111 011 101 110 # the top vertex
|
empty line, ignored
vertex with label 001 is adjacent
to vertices with labels 000,
011, and 101
the top vertex is advacent to 3 vertices
|
Last modified: Mon, Jan 23, 2023.
