Isoperimetric Tools

Solution of the MWI/MRI problem

Let P be a ranked poset with a weight function w : P -> R. For a subset A of P denote by w(A) the sum of weights of elements of A. The subset A is called ideal if for every element x of A all elements preceeding x in the partial order are in A. It is easily seen that for every m = 1 . . |P| there exists an ideal of size m.

The Maximum Weight Ideal (MWI) problem consists of finding for a given m an ideal A of P such that |A| = m and w(A) is maximum among all ideals of size m. This maximum value of the weight is denoted by w(m). The Maximum Rank Ideal (MRI) problem is a special case of the MWI problem with the weight function being equal to the poset rank function.

Both problems have numerous applications to extremal poset problems [3], to edge-isoperimetric problems of graphs [2], and to many other optimization problems on graphs and posets. The MWI and MRI problems are NP-complete, so there is no much hope for an efficient solution of them. The program is based on an algorithm from [1] for generating all ideals in a poset. Furthermore, the program checks whether or not the poset admits nested solutions. If nested solutions exist, one of optimal total orders is computed. Otherwise, a longest initial series of nested solutions is output.

• To solve the MRI problem, your poset must be encoded as a non-weight one and must be ranked by the nature of the problem. In this case make sure to uncheck the "weighed" box in the uploading dialog.
• To solve the MWI problem, your poset must be encoded as a weighted one and must be ranked for the current version of the tool. Make sure to check the "weighed" box in the poset uploading dialog.

References

[1] X. Berenguer, L.H. Harper: Estabilizacion y resolucion de algunos problemas combinatorios en grafos simetricos, Questio, vol. 3 (1979), No. 2, 105-117.

[2] S.L. Bezrukov: On an equivalence in discrete extremal problems, Discr. Math., vol. 203, 1999, no. 1, 9-22.

[3] K. Engel: Sperner theory, Cambridge University Press, 1997.

Select a file to upload

Poset encoding instructions

Encoding of non-weighted posets

The poset file is a text (ASCII) file with the number of lines equal to the number of poset elements, that is one line per element. For each element p of P the corresponding line must contain the following information on p:

Here:

Moreover, the file must satisfy the following claims:

Example

Poset	Encoding	Comments
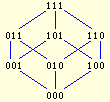	000 # the bottom vertex 001 000 # first level 010 000 100 000 011 001 010 # second level 101 001 100 110 010 100 111 011 101 110 # the top level	000 is the label empty line, ignored vertex 001 covers 000 vertex 010 covers 000 vertex 100 covers 000 vertex 011 covers 001 and 010 vertex 101 covers 001 and 100 vertex 110 covers 010 and 100 the top vertex covering 3 other vertices

Check Gallery of Posets for more examples.

Encoding of weighted posets

The encoding in this case is similar to the one above. The only difference is that every line of text must contain information on the weight of the corresponsing poset element.

The poset file is a text (ASCII) file with the number of lines equal to the number of poset elements, that is one line per element. For each element p of P the corresponding line must contain the following information on p:

Here:

Moreover, the file must satisfy the following claims:

Example

Poset	Encoding	Comments
	000 1 # the bottom vertex 001 1 000 # first level 010 2 000 100 -1 000 011 3 001 010 # second level 101 3 001 100 110 2 010 100 111 1 011 101 110 # the top level	000 is the label, 1 is the weight empty line, ignored vertex 001 covers 000 vertex 010 covers 000 vertex 100 covers 000 and has negative weight vertex 011 covers 001 and 010 vertex 101 covers 001 and 100 vertex 110 covers 010 and 100 the top vertex covering 3 other vertices

Last modified: Mon, Jan 23, 2023.