For a graph G and a subset A of its vertices denote by Bdry(A) the set of vertices of the complement that are at distance 1 from A. Furthermore, denote by Ball(A) the ball around A, i.e. the union of A and Bdry(A).
This tool computes and displays the boundary of a subset of GxH. The graphs G and H are defined by their ball-sequences. The i-th element of such sequence is the minimum size of the ball around a set of size i, for i=1, 2, ... , |G|.
We assume here that the graphs are connected. This means that the ball-sequence is not decreasing, and the i-th entry is at least min(i+1, |G|), for i=1, 2, ... , |G|.
The ball-sequence does not specify the graph uniquely. Moreover, not any ball-sequence satisfying the above properties is realized by some graph. However, any such sequence is realized by an oriented graph. In this case the boundary is defined as the set of vertices that can be reached from A by outgoing edges. The oriented graph is obtained by connecting the vertex i with the vertices 1, 2, ..., Ball(i) for i=1, 2, ... , |G|.
Enter the ball-sequences into the corresponding text input fields (separate its entries by spaces) and click the "Show GxH" button. You will see a grid with each cell corresponding to a vertex of GxH with G represented by columns and H by rows. The cell in the bottom left corner represents the vertex (1,1). Clicking a cell toggles its belonging to the set, which is indicated by coloring the cell in blue. The boundary vertices are shown in green.
You also can upload one or both files and combine uploading with entering the ball-sequences. The graph encoding instructions are at the bottom of this page. In case of uploading of at least one file, use the "Browse..." button, then click "Upload" button, and then "Show GxH". If one of the files does not need to be uploaded, just leave its field empty. Entering a ball-sequence followed by "Enter" key will reset the file data for this graph.
The graphs are encoded by using the adjacency list represenation. The graph file is a text (ASCII) file with the number of lines equal to the number of vertices, that is one line per vertex. For each vertex v of G the corresponding line must contain the following information:
Here:
Moreover, the file must satisfy the following claims:
| Graph | Encoding | Comments |
|---|---|---|
 |
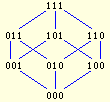000 001 010 100 # the bottom vertex 001 000 011 101 # first level 010 000 011 110 100 000 101 110 011 001 010 111 # second level 101 001 100 111 110 010 100 111 111 011 101 110 # the top vertex |
empty line, ignored vertex with label 001 is adjacent to vertices with labels 000, 011, and 101 the top vertex is advacent to 3 vertices |
Last modified: Mon, Jan 23, 2023.